Dans cet article, je vous présente 5 algorithmes que je trouve très intéressants, tant par leur beauté mathématique que par leur utilité. Il n’est pas nécessaire d’avoir un bon niveau en mathématiques ou en programmation pour comprendre les bases des idées ci-dessous.
Table des matières
La formule de Luhn
Cette formule est pour le moins étonnante puisqu’elle permet de générer des numéros de cartes bleues valides ! La formule de Luhn est ce qu’on appelle une formule de somme de contrôle. Cette fonction permet de détecter une erreur lors de la transmission d’une donnée. Le numéro de votre carte bleue par exemple, composée de 4 séries de 4 chiffres obéit à la formule de Luhn. La formule est très simple à utiliser :
Imaginez que vous souhaitiez vérifier que 4813 4514 9414 4557 est un numéro de carte bleu valide. À première vue il semblerait que oui puisqu’il est bien composé de 16 chiffres. Pour vérifier avec la formule de Luhn il faut procéder comme ceci :
Tout d’abord, on réécrit le numéro dans un tableau
| Étape 1 | 4 | 8 | 1 | 3 | 4 | 5 | 1 | 4 | 9 | 4 | 1 | 4 | 4 | 5 | 5 | 7 |
On double ensuite un nombre sur deux en partant de l’avant-dernier :
| Étape 1 | 4 | 8 | 1 | 3 | 4 | 5 | 1 | 4 | 9 | 4 | 1 | 4 | 4 | 5 | 5 | 7 |
| Étape 2 | 8 | 8 | 2 | 3 | 8 | 5 | 2 | 4 | 18 | 4 | 2 | 4 | 8 | 5 | 10 | 7 |
Maintenant on fait une nouvelle ligne « Étape 3 » en reportant les chiffres de l’étape 2, sauf si le chiffre est supérieur à 9, auquel cas il faut retrancher à ce chiffre 9.
| Étape 1 | 4 | 8 | 1 | 3 | 4 | 5 | 1 | 4 | 9 | 4 | 1 | 4 | 4 | 5 | 5 | 7 |
| Étape 2 | 8 | 8 | 2 | 3 | 8 | 5 | 2 | 4 | 18 | 4 | 2 | 4 | 8 | 5 | 10 | 7 |
| Étape 3 | 8 | 8 | 2 | 3 | 8 | 5 | 2 | 4 | 9 | 4 | 2 | 4 | 8 | 5 | 1 | 7 |
Et voilà, maintenant il ne reste plus qu’à faire la somme des chiffres de cette dernière étape : 8+8+2+3+8+5+2+4+9+4+2+4+8+5+1+7 = 80. Si la somme est divisible par 10 (si le nombre se termine par un 0 du coup), alors le numéro est bon. Ici, 80 est divisible par 10, c’est donc potentiellement un numéro valide. Essayez en changeant un numéro avec un autre et vous aurez de grandes chances de ne plus avoir un numéro valide au sens de Luhn ! La vérification par la méthode de Luhn est également appelée somme de contrôle par modulo 10 : on vérifie que le résultat final est bien un multiple de 10.
Les formules de somme de contrôle (checksum en anglais) sont intensivement utilisées sur Internet pour vérifier que le fichier que vous téléchargez n’a pas été corrompu ou que la page web que vous consultez n’a pas été altérée par une personne malintentionnée.
Cet algorithme est également utilisé dans l’administration française pour déterminer les numéros SIRET par exemple ou encore dans les téléphones pour générer le numéro IMEI. Vous pouvez d’ailleurs vous amusez à vérifier le numéro IMEI de votre téléphone puisqu’il vous suffit de taper *#06# sur le clavier servant à composer un numéro, pour l’afficher (pas besoin d’appuyer sur la touche pour appeler).
Création d’un labyrinthe (Depth-first search)
Comment les labyrinthes sont-ils construits ? Trouver un algorithme permettant de construire un labyrinthe n’est pas une chose aisée : la solution triviale qui consisterait à partir d’une salle vide de la remplir de murs positionnés aléatoirement ne fournit pas un véritable labyrinthe.
Je vais vous présenter ici un algorithme simple permettant de réaliser un labyrinthe. Cet algorithme a l’avantage d’être généralisable à une grille à n-côtés, on peut donc créer des labyrinthes sur une grille à base de carrés (cas le plus courant), mais aussi sur des grilles à base d’hexagones par exemple !
L’algorithme se résume en pseudo-code à cet enchainement :
- Créer une pièce de la taille voulue, remplie de murs pour chaque case (donc en haut, en bas, à droite et à gauche si la grille est rectangulaire)
- Chaque case a une propriété booléenne (vrai/faux) que nous appellerons « visitée ». On initialise toutes les cases à « visitée » = faux. De plus, nous allons avoir besoin d’une pile, vide au départ.
- Choisir une case de départ (en général en haut à gauche) et la marquer comme « visitée » (= vrai)
- Tant qu’il y a des cases non visitées :
- Si la cellule a des voisins qui n’ont pas été visités :
- Choisir de manière aléatoire un des voisins
- Mettre sur la pile la case actuelle
- Supprimer le mur entre la case actuelle et la case choisie en 1.
- La case choisie devient la case actuelle et on la marque comme « visitée ».
- Si tous les voisins de la cellule actuelle ont été visités :
- Sortir une case de la pile
- Cette case devient la case actuelle
- Si la cellule a des voisins qui n’ont pas été visités :
Cet algorithme peut être visualisé ci-dessous :
En bleu, la case n’est pas visitée, en orange la case est visitée et en vert tous les voisins de la cellule ont été visités.
Si vous voulez en apprendre plus sur les différents algorithmes de création de labyrinthes, je vous conseille l’excellente page Wikipédia sur le sujet (en anglais).
Formule du double pendule
Si vous ne connaissez pas encore le double pendule, je vous renvoie à la célèbre vidéo du Dr. Nozman :
Les mouvements issus de cet objet sont chaotiques… mais il est tout de même possible de les simuler ! En effet, comme le pendule classique, le double pendule a aussi sa formule ! Si ça vous intéresse, continuez la lecture pour implémenter votre propre simulateur de double pendule.
Pour commencer, définissons quelques notations :
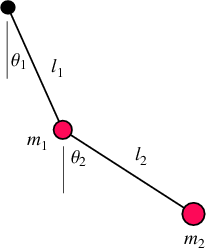
Nous avons 6 variables :
- Thêta 1 : l’angle formé entre l’axe du pendule et le premier poids
- L1 : la longueur de la première tige
- m1 : la masse du premier poids
- Thêta 2 : l’angle formé entre le premier poids et le deuxième poids
- L2 : la longueur de la deuxième tige
- m2 : la masse du deuxième poids
À ces 6 variables, s’ajoutent évidemment la constante gravitationnelle, notée G, qui équivaut à 9.81 sur notre bonne vieille planète Terre.
Maintenant, comment tracer le pendule ? Nous pouvons initialiser nos 6 variables à des valeurs par défaut. Seulement, comment le modèle évoluera à travers le temps ? À vrai dire, il n’y a que les angles (Thêta 1 et Thêta 2) qui vont évoluer avec le temps. Nous cherchons la valeur de ces angles après un certain pas de temps, nous voulons donc obtenir une accélération. Et qui dit accélération, dit dérivée seconde ! Le système initial est résoluble grâce aux équations qui suivent, donnant les valeurs de Thêta 1 et 2 à travers le temps :
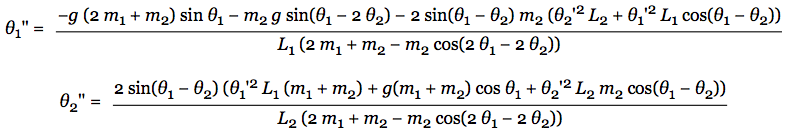
Vous n’avez plus qu’à utiliser ces 2 formules avec votre langage de programmation préféré et une bibliothèque de dessin ! Il est également possible de multiplier les valeurs des angles par un coefficient constant approximativement égal à 0.99 pour simuler les frottements de l’air (et faire en sorte que le pendule s’arrête au bout d’un moment).
Si ça vous intéresse, vous pouvez vous amuser directement dans votre navigateur à jouer avec un double pendule : https://www.myphysicslab.com/pendulum/double-pendulum-en.html. De plus, sachez qu’il est également possible de simuler les mouvements d’un triple pendule : mais les équations sont beaucoup plus longues ! La simulation d’un pendule plus long nécessiterait (sûrement?) l’utilisation d’un moteur physique, comme Box2D.
La congruence de Zeller
La formule qui suit est intéressante, car elle permet de connaître le jour de la semaine (lundi, mardi …) à partir de la date. Si je vous dis, quel jour fut le 10 décembre 1815 ? La congruence de Zeller permet d’en connaitre la réponse ! Le mathématicien allemand Christian Zeller a inventé 2 formules : l’une pour le calendrier grégorien (celui que nous utilisons tous les jours) et l’autre pour le calendrier julien, qui fut utilisé dans la Rome Antique.
La formule pour le calendrier grégorien est la suivante :
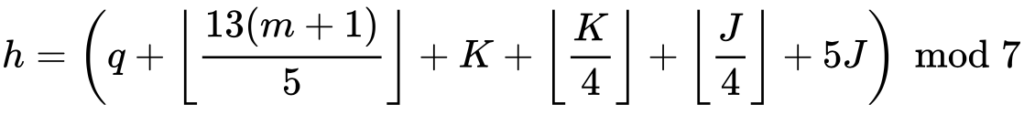
Avec h le jour de la semaine, allant de 0 à 6 (0 étant samedi, 6 étant vendredi), q est le jour du mois, m est le mois allant de 3 à 14 (3 étant mars et 14 étant février), K étant l’année modulo 100 (donc pour l’année 2018, K=18) et J étant l’année / 100, tronqué à l’unité (donc l’année 1987 devient 19). Attention, il y a une exception si le mois de votre date est janvier ou février, il faut utiliser non pas l’année de votre date, mais l’année de votre date – 1.
Essayons la formule avec la date d’aujourd’hui, le 25 février 2018.
On a q = 25, m = 14, K = 17 (c’est l’exception) et J = 20, ce qui nous donne :
h = ( 25 + [(13x(14+1)) / 5] + 17 + [17/4] + [20/4] + 5×20 ) % 7, d’où h = 1.25, après troncature, on obtient bien h = 1 = dimanche ! Notez que l’on peut améliorer la formule pour qu’elle retourne h compris entre 1 et 7, 1 étant lundi et 7 étant dimanche. Pour ça, il suffit de faire (h + 5) % 7 + 1.
Évidemment la formule est impossible à réaliser de tête, mais est à la portée de n’importe quel ordinateur.
Si vous voulez comprendre d’où vient cette formule, lisez la page Wikipédia dédiée.
La méthode du classement Elo
Il s’agit de la méthode qui permet d’établir le classement des joueurs d’échecs. Elle fut inventée par Arpad Elo et ce système d’évaluation peut s’adapter à tous les autres jeux à deux joueurs ou plus. Le classement Elo est par exemple utilisé pour classer les joueurs du jeu vidéo League of Legends ou Counter Strike. On retrouve également la formule dans le film The Social Network, qui aurait permis à Mark Zuckerberg, fondateur de Facebook, d’établir un classement « d’attractivité » des utilisatrices du site. Bref, vous l’aurez compris, la méthode de classement Elo est très utilisée.
Mais comment classer deux joueurs ? L’idée principale est de comparer leur force relative : un joueur jugé plus fort qu’un autre aura, logiquement, plus de chance de gagner un match. Le joueur qui gagne le match gagnera d’autant plus de place que la différence de niveau entre lui et son adversaire est grande.
La formule du prochain score Elo d’un joueur à l’issue d’un match est la suivante :
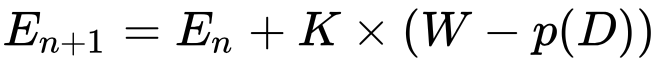
Quelles sont les variables entrant en jeu ?
Nous avons En qui est l’ancien score Elo du joueur.
K est un facteur permettant de contrôler la volatilité du classement. Un K élevé va permettre à de nouveaux bons joueurs de gagner plus rapidement des points et ainsi trouver un score Elo les représentant plus rapidement. Aux échecs, K = 40 pour les 30 premières parties d’échecs jouées puis passe à 20 tant que le joueur n’a pas plus de 2400 points, puis K = 10 au-delà.
Ensuite, W est le résultat de la partie jouée : il vaut 1 pour une victoire, 0 pour une défaite et 0,5 si la partie s’est finie par un match nul.
p(D) est la partie la plus intéressante de la formule : il s’agit de la probabilité de gagner le match en tenant compte de la différence de score Elo des joueurs, notée D. Ainsi, p(D) tend logiquement vers 1 quand le joueur testé a un bien meilleur score Elo que son adversaire et réciproquement, vers 0 quand le joueur testé a un niveau plus faible que son adversaire (on ne s’attend pas à ce qu’il gagne le match).
Ainsi, W – p(D) représente l’écart entre le résultat effectif et le résultat attendu : si la différence est faible, le prochain score Elo du joueur ne changera pas beaucoup. Maintenant, vous vous posez sûrement la question de la forme de la fonction p(D). p(D) doit nécessairement être compris entre 0 et 1 et être centré pour D=0. Au départ, Arpad Elo a proposé d’utiliser la fonction de répartition de la loi normale. Cependant, il s’est avéré que la probabilité de gagner un match en fonction de la différence de niveau est plus étalée que ce que la loi normale propose. La Fédération Internationale des échecs (FIDE) a alors proposé d’utiliser une fonction basée sur une loi logistique, et plus précisément cette fonction :
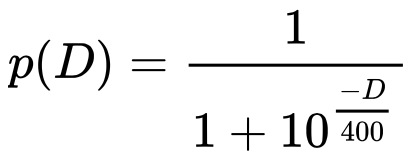

Pourquoi 400 dans la fonction de répartition ? C’est un seuil que la FIDE a décidé d’utiliser : il revient à dire que si l’écart entre les 2 scores est égal à 400, les probabilités de victoires sont statistiquement significatives (1/(1+10^(-400/400)) = 90%). C’est donc la différence de score Elo maximale permise pour jouer une partie classée.
Maintenant, que nous savons calculer le prochain classement d’un joueur, comme déterminer son premier classement ? Il existe plusieurs méthodes, la plus simple étant de prendre un seuil initial fixé à 1000 par exemple, mais il est également d’utiliser une technique plus élégante. Il suffit de prendre la réciproque de la fonction de répartition :
Le joueur non classé doit jouer par exemple 10 parties contre des joueurs classés. On calcule la moyenne du niveau des joueurs et le taux de victoire du joueur non classé et il nous suffit d’appliquer la formule. Imaginons que le niveau moyen des joueurs fut de 1800 et que le joueur gagna 6 matchs sur 10. Le premier classement du joueur sera donc de 1800 + 400xlog(0.6/(1-0.6)) = 1870.
La beauté de cette méthode de classement est telle que la probabilité de gagner pour un joueur de score 2500 contre un joueur de score 2400 est la même que pour un joueur de score 1600 contre un joueur de score 1500 par exemple.
Conclusion
Il y a beaucoup d’autres algorithmes intéressants qui mériteraient d’être cités ici. Si le sujet vous intéresse, je vous propose d’autres pistes d’exploration possibles, en vrac :
- Les algorithmes de tris, notamment le bubble-sort (vous trouverez beaucoup de visualisations de l’algorithme sur Internet)
- Les algorithmes liés au raytracing – ou comment les images de synthèse sont crées
- Simulation des couleurs du ciel avec le modèle de Nishita (attention le niveau en mathématiques est élevé)
- Le perceptron : la base du machine learning.
- KNN : qui est un algorithme de clustering et classification, très simple à comprendre.
- Les automates cellulaires, comme le fameux Conway Game of Life ou le moins connu Langton’s Ant & Termite.
- L’inversion d’une matrice par la méthode de Gauss-Jordan.
- Le Seam Carving : cet algorithme permet de réduire ou agrandir une image sans changer les proportions des sujets importants ! (le lien comporte des images de démonstration)



Impressionnant